Test for prime numbers using python!

• 29-05-2018
• programming

Share:

https://techconductor.com/blogs/programming/prime_finder.php

Copy

A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number.

For example, 3 is prime because the only ways of writing it as a product is: 1 × 3 or 3 × 1, involve 3 itself. However, 4 is composite because it is the product of two numbers (2 × 2) that are both smaller than 3.

primality test is an algorithm for determining whether an input number is prime. Among other fields of mathematics, it is used for cryptography.

The simplest primality test is trial division: Given an input number n, check whether any prime integer j from 2 to √n evenly divides n such that the division leaves no remainder. If n is divisible by any j then n is composite, otherwise it is prime.

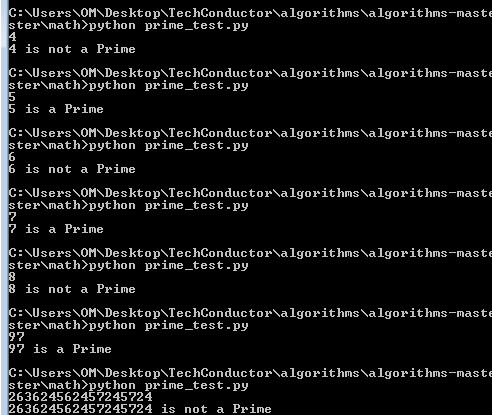
Here is a simple python function to test whether a given number is a prime or not.

The code works efficiently when testing for a specific number.

The function takes an input and checks whether the number ia a prime or not.

#prime_test function.
def prime_test(n): #n is the number passed to check for prime
    
    if n <= 1:
        print(str(n) + ' is not a Prime') #prints n is not a prime and end the function
        return False

    if n == 2 or n == 3:
        print(str(n) + ' is a Prime') #prints n is a prime and end the function
        return True

    if n % 2 == 0 or n % 3 == 0:
        print(str(n) + ' is not a Prime') #prints n is not a prime and end the function
        return False

    j = 6
    while (j * j < n):
        if n % (j - 1) == 0 or n % (j + 1) == 0:
            print(str(n) + ' is not a Prime') #prints n is not a prime and end the function
            return False
        j += 6

    print(str(n) + ' is a Prime') #prints n is a prime and end the function
    return True

#call the prime_test function and provide a number.
prime_test(int(input()))

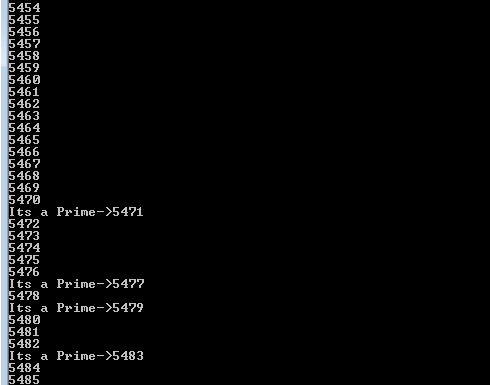
Here is the output of the function when given few specific numbers to test.

Although we can use a for loop to iterate over a range of numbers and test each of them for prime, but that won't be an efficient code. Here is an example using a for loop to do the above task.

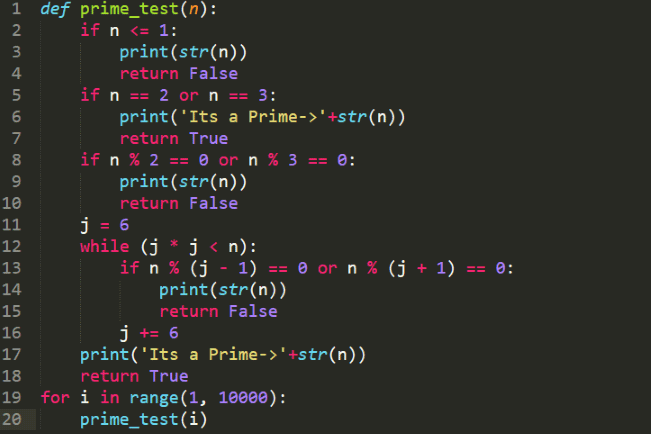
Result: Works but slow and memory intensive.

Hope you guys! found it helpful and do share the post also subscribe to Tech Conductor on one click below.